ISI MMath Solutions and Discussion 2017 : PMB
ISI MMath PMB 2017 Subjective Questions along with hints and solutions and discussions
To view ISI MMATH 2020 solutions, hints, and discussions: Click Here
To view ISI MMATH 2019 solutions, hints, and discussions: Click Here
To view ISI MMATH 2018 solutions, hints, and discussions: Click Here
To view ISI MMATH 2016 solutions, hints, and discussions: Click Here
To view previous year’s question papers: Click Here
Group A
Problem 1.
Let ![]() , such that
, such that ![]() and
and ![]() as
as ![]() . Let
. Let ![]() . Show that
. Show that ![]() .
.
Topic: Real Analysis, Difficulty level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 1 Hints along with Solution & Discussion
Hint 1
Use the representation
![]()
Fix any ![]() There exists
There exists ![]() such that for all
such that for all ![]()
![Rendered by QuickLaTeX.com \[\left|\sum^m_{n=1}a_n-a\right|<1\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-73fd6794b6505fec5c801180b4001b47_l3.png)
Hint 2
![]()
Hint 3
Then for all ![]() we have
we have
![]()
Full Solution
We use the representation
![]()
Fix any ![]() There exists
There exists ![]() such that for all
such that for all ![]()
![Rendered by QuickLaTeX.com \[\left|\sum^m_{n=1}a_n-a\right|<1, \mbox{ and }\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-82464f2f70cdf842d7aab5b616e0b1f5_l3.png)
![]()
Then for all ![]() we have
we have
![]()
![Rendered by QuickLaTeX.com \[=\frac{1}{2}a+\frac{1}{2}\left(\sum^m_{n=1}a_n-a\right)+\frac{1}{2}\sum^m_{n=1}|a_n|\geq\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-0ed31c32c3c1905abfaaed3b3d8f1ec7_l3.png)
![Rendered by QuickLaTeX.com \[\geq \frac{1}{2}\sum^m_{n=1}|a_n|-\frac{1}{2}|a|-\frac{1}{2}\left|\sum^m_{n=1}a_n-a\right|>\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-b668222f97b16a044d0277bcf550f330_l3.png)
![]()
For any ![]() there exists
there exists ![]() such that for all
such that for all ![]()
![]()
In other words, ![]()
Problem 2.
Let ![]()
![]() . Prove that there exists
. Prove that there exists ![]() such that
such that ![]() for all
for all ![]() .
.
Topic: Real Analysis, Difficulty Level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 2 Hints along with Solution & Discussion
Hint 1
Apply the arithmetic mean-geometric mean inequality:
for all ![]() and
and ![]()
![]()
Hint 2
Let ![]()
![]()
![]()
![]() where
where ![]() Then
Then
![]()
Hint 3
Take
![]()
Full Solution
We apply the arithmetic mean-geometric mean inequality:
for all ![]() and
and ![]()
![]()
Let ![]()
![]()
![]()
![]() where
where ![]() Then
Then
![]()
So, for any ![]() we have
we have
![]()
Take
![]()
Then
![]()
for any ![]() The answer is
The answer is
![]()
Problem 3.
Let ![]() be an increasing function. Suppose there are sequences
be an increasing function. Suppose there are sequences ![]() and
and ![]() such that
such that ![]() for all
for all ![]() and
and ![]() as
as ![]() . Prove that
. Prove that ![]() is continuous at
is continuous at ![]() .
.
Topic: Real Analysis, Difficulty Level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 3 Hints along with Solution & Discussion
Hint 1
Try to form the mathematical expression with ![]() and
and ![]() from this given statement:
from this given statement:
“Suppose there are sequences ![]() and
and ![]() such that
such that ![]() for all
for all ![]() and
and ![]() as
as ![]() “.
“.
Hint 2
Let ![]() There exists
There exists ![]() such that for all
such that for all ![]()
![]()
Hint 3
Fix such ![]() and take
and take ![]() Consider arbitrary
Consider arbitrary ![]()
![]() If
If ![]() then
then ![]()
![]()
and
![]()
If ![]() then
then ![]()
![]()
Full Solution
Let ![]() There exists
There exists ![]() such that for all
such that for all ![]()
![]()
Fix such ![]() and take
and take ![]() Consider arbitrary
Consider arbitrary ![]()
![]() If
If ![]() then
then ![]()
![]()
and
![]()
If ![]() then
then ![]()
![]()
and
![]()
In any case,
![]()
as soon as ![]()
![]() is continuous at
is continuous at ![]()
Problem 4.
Do there exist continuous functions ![]() and
and ![]() on [0,1] such that
on [0,1] such that ![]() is a solution to
is a solution to ![]() on
on ![]() for all
for all ![]() justify your answer.
justify your answer.
Topic: Elements of Ordinary Differential Equations, Difficulty Level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 4 Hints along with Solution & Discussion
Hint 1
Assume that such functions exist and then proceed.
Hint 2
Derivatives of ![]() are equal to
are equal to
![]()
Hint 3
In particular,
![]()
Full Solution
Assume that such functions exist. Derivatives of ![]() are equal to
are equal to
![]()
In particular,
![]()
If for all ![]() the equality
the equality
![]()
then taking the limit as ![]() we get
we get
![]()
which is impossible. So, such functions ![]() and
and ![]() do not exist.
do not exist.
Problem 5.
Let ![]() be defined by
be defined by
![Rendered by QuickLaTeX.com \[f(x)=\int^{1+e^{x^3+x}}_{e^{x^3+x}} e^{r^2} dr\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-6d3917094353e923224c39a2bd82a82b_l3.png)
for all ![]() . Prove that
. Prove that ![]() is monotone.
is monotone.
Topic: Real Analysis, Difficulty Level: Easy
Indian Statistical Institute, ISI MMath 2017 Problem 5 Hints along with Solution & Discussion
Hint 1
Observe the relation
![]()
where ![]()
![]()
Hint 2
We have
![]()
Hint 3
![]()
Full Solution
Observe the relation
![]()
where ![]()
![]() We have
We have
![]()
![]()
In particular, ![]() for
for ![]() Since
Since ![]() we have
we have ![]()
![]() and
and
![]()
The function ![]() is strictly increasing.
is strictly increasing.
Problem 6.
Let ![]() be an
be an ![]() symmetric matrix with non-negative real entries such that
symmetric matrix with non-negative real entries such that ![]() if and only if
if and only if ![]() . Show that
. Show that ![]() is a metric on
is a metric on ![]() .
.
Topic: Metric Space, Difficulty Level: High
Indian Statistical Institute, ISI MMath 2017 Problem 6 Hints along with Solution & Discussion
Hint 1
At first we verify that the minimum is achieved. Consider a path ![]() between
between ![]() and
and ![]() of length
of length ![]() Among elements
Among elements
![]()
there are at least two identical elements: ![]() for some
for some ![]() Then
Then
![]()
is a path of length ![]() Also,
Also, ![]() and
and
![Rendered by QuickLaTeX.com \[\sum^{k-1}_{l=0}w(i_l,i_{l+1})\geq \sum^{r-2}_{l=0}w(i_l,i_{l+1})+w(i_{r-1},i_s)+\sum^{k-1}_{l=s}w(i_l,i_{l+1}).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-bfbe0bb7988f78947ee167b67443a58c_l3.png)
It means that it is enough to consider only paths of length ![]() There are only finitely many such paths, hence the minimum in the definition of
There are only finitely many such paths, hence the minimum in the definition of ![]() is achieved. We check axioms of a metric.
is achieved. We check axioms of a metric.
Hint 2
For any path ![]() between
between ![]() and
and ![]() we have
we have
![Rendered by QuickLaTeX.com \[\sum^{k-1}_{l=0}w(i_l,i_{l+1})\geq 0.\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-debb93d067bf85e4c32e13f9341ea690_l3.png)
Hence, ![]() Assume
Assume ![]() Since the minimum in the definition of
Since the minimum in the definition of ![]() is achieved, we have
is achieved, we have
![Rendered by QuickLaTeX.com \[\sum^{k-1}_{l=0}w(i_l,i_{l+1})= 0 \eqno(*)\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-b3150955a0b09cc752c7e283e14fee0a_l3.png)
for some path ![]() between
between ![]() and
and ![]() Since all terms in the left-hand side of (*) are non-negative, we deduce that
Since all terms in the left-hand side of (*) are non-negative, we deduce that
![]()
By definition of ![]() it follows that
it follows that
![]()
In particular, ![]() We’ve proved that
We’ve proved that ![]() and
and ![]()
Hint 3
Consider a path ![]() Then
Then ![]() But
But ![]() hence
hence
![]()
This proves that ![]()
Full Solution
At first we verify that the minimum is achieved. Consider a path ![]() between
between ![]() and
and ![]() of length
of length ![]() Among elements
Among elements
![]()
there are at least two identical elements: ![]() for some
for some ![]() Then
Then
![]()
is a path of length ![]() Also,
Also, ![]() and
and
![Rendered by QuickLaTeX.com \[\sum^{k-1}_{l=0}w(i_l,i_{l+1})\geq \sum^{r-2}_{l=0}w(i_l,i_{l+1})+w(i_{r-1},i_s)+\sum^{k-1}_{l=s}w(i_l,i_{l+1}).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-bfbe0bb7988f78947ee167b67443a58c_l3.png)
It means that it is enough to consider only paths of length ![]() There are only finitely many such paths, hence the minimum in the definition of
There are only finitely many such paths, hence the minimum in the definition of ![]() is achieved. We check axioms of a metric.
is achieved. We check axioms of a metric.
- For any path
 between
between 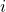 and
and 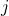 we have
we have
![Rendered by QuickLaTeX.com \[\sum^{k-1}_{l=0}w(i_l,i_{l+1})\geq 0.\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-debb93d067bf85e4c32e13f9341ea690_l3.png)
Hence, ![]() Assume
Assume ![]() Since the minimum in the definition of
Since the minimum in the definition of ![]() is achieved, we have
is achieved, we have
![Rendered by QuickLaTeX.com \[\sum^{k-1}_{l=0}w(i_l,i_{l+1})= 0 \eqno(*)\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-b3150955a0b09cc752c7e283e14fee0a_l3.png)
for some path ![]() between
between ![]() and
and ![]() Since all terms in the left-hand side of (*) are non-negative, we deduce that
Since all terms in the left-hand side of (*) are non-negative, we deduce that
![]()
By definition of ![]() it follows that
it follows that
![]()
In particular, ![]() We’ve proved that
We’ve proved that ![]() and
and ![]()
- Consider a path
 Then
Then 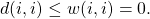 But
But 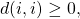 hence
hence
![]()
This proves that ![]()
- Consider a path
 between
between 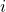 and
and 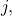 such that
such that
![Rendered by QuickLaTeX.com \[d(i,j)=\sum^{k-1}_{l=0}w(i_l,i_{l+1}).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-111674179446868ca76874098292ac07_l3.png)
Observe that ![]() is a path between
is a path between ![]() and
and ![]() So,
So,
![Rendered by QuickLaTeX.com \[d(j,i)\leq \sum^{k-1}_{l=0}w(i_{k-l},i_{k-l+1})=\sum^{k-1}_{l=0}w(i_{l+1},i_{l})=\sum^{k-1}_{l=0}w(i_{l},i_{l+1})=d(i,j).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-dfddaf3143df7116fdfada2868e74a7d_l3.png)
We’ve proved that
![]()
Since this is true for all ![]() we also get
we also get
![]()
Finally, ![]()
- Consider two paths

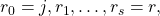 such that
such that
![Rendered by QuickLaTeX.com \[d(i,j)=\sum^{k-1}_{l=0}w(i_l,i_{l+1}), d(j,r)=\sum^{s-1}_{p=0}w(r_p,r_{p+1}).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-9d89ffa62518e65381ef0b19f465efd7_l3.png)
Observe that ![]() is a path between
is a path between ![]() and
and ![]() Hence
Hence
![Rendered by QuickLaTeX.com \[d(i,r)\leq \sum^{k-1}_{l=0}w(i_j,i_{j+1})+w(i_k,r_1)+\sum^{s-1}_{p=1}w(r_p,r_{p+1})=\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-2aa17a6e3b1f5ed41b4b3d78e2e01c7f_l3.png)
use that ![]()
![Rendered by QuickLaTeX.com \[=\sum^{k-1}_{l=0}w(i_j,i_{j+1})+\sum^{s-1}_{p=0}w(r_p,r_{p+1})=d(i,j)+d(j,r).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-3b93cbd3d5aea494d24366d8c680d3b1_l3.png)
The triangle inequality is proved.
![]() is a metric on
is a metric on ![]()
Group B
Problem 7.
Factory ![]() produces
produces ![]() bad watch in
bad watch in ![]() and factory
and factory ![]() produces
produces ![]() bad watch in
bad watch in ![]() . You are given two watches from one of the factories and you don’t know which one.
. You are given two watches from one of the factories and you don’t know which one.
- What is the probability that the second watch works?
- Given that the first watch works, what is the probability that the second watch works

Topic: Probability Theory, Difficulty Level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 7 Hints along with Solution & Discussion
Hint 1
Introduce two hypothesis
![]()
![]()
Hint 2
Then ![]() Consider events
Consider events
![]()
![]()
It is given that ![]()
![]()
Hint 3
By the law of total probability
![]()
Full Solution
Introduce two hypothesis
![]()
![]()
Then ![]() Consider events
Consider events
![]()
![]()
It is given that ![]()
![]()
- By the law of total probability
![]()
- We compute the probability
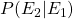 by the definition:
by the definition:
![]()
From the previous part, we know ![]() By the law of total probability
By the law of total probability
![]()
So,
![]()
Problem 8.
Let ![]() be a commutative ring containing a field
be a commutative ring containing a field ![]() as a sub-ring. Assume that
as a sub-ring. Assume that ![]() is a finite dimensional
is a finite dimensional ![]() -vector space. Show that every prime ideal of
-vector space. Show that every prime ideal of ![]() is maximal.
is maximal.
Topic: Abstract Algebra- Ring and Field Theory, Difficulty Level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 8 Hints along with Solution & Discussion
Hint 1
Let ![]() be a prime ideal in
be a prime ideal in ![]() . It is enough to check that
. It is enough to check that ![]() is a field
is a field
Hint 2
The infinite sequence ![]() is linearly dependent and there exists samllest
is linearly dependent and there exists samllest ![]() such that
such that
![]()
for some non-zero coefficients ![]() If
If ![]()
Hint 3
Then
![]()
Full Solution
Let ![]() be a prime ideal in
be a prime ideal in ![]() . It is enough to check that
. It is enough to check that ![]() is a field, i.e. every nonzero element of
is a field, i.e. every nonzero element of ![]() has a multiplicative inverse.
has a multiplicative inverse. ![]() is a finite-dimensional
is a finite-dimensional ![]() -vector space. Hence the infinite sequence
-vector space. Hence the infinite sequence ![]() is linearly dependent and there exists smallest
is linearly dependent and there exists smallest ![]() such that
such that
![]()
for some non-zero coefficients ![]() If
If ![]() then
then
![]()
Let ![]() be a representative of
be a representative of ![]() Then
Then
![]()
![]() hence
hence ![]() The ideal
The ideal ![]() is prime, so
is prime, so
![]()
and
![]()
The latter contradicts minimality of ![]() So,
So, ![]() and
and
![]()
![]() has a multiplicative inverse.
has a multiplicative inverse. ![]() is a field and
is a field and ![]() is a maximal ideal.
is a maximal ideal.
Problem 9.
Let ![]() be prime numbers and
be prime numbers and ![]() such that
such that ![]() then show that
then show that ![]() .
.
Topic: Number Theory, Difficulty Level: Easy
Indian Statistical Institute, ISI MMath 2017 Problem 9 Hints along with Solution & Discussion
Hint 1
By assumptions of the problem ![]()
Hint 2
Let ![]() be the order of
be the order of ![]() modulo
modulo ![]() i.e.
i.e. ![]() is the smallest positive integer such that
is the smallest positive integer such that ![]()
Hint 3
From ![]() we deduce that
we deduce that ![]()
![]() is prime, so
is prime, so ![]()
Now use “Fermat’s Little Theorem”.
Full Solution
By assumptions of the problem ![]() Let
Let ![]() be the order of
be the order of ![]() modulo
modulo ![]() i.e.
i.e. ![]() is the smallest positive integer such that
is the smallest positive integer such that ![]() From
From ![]() we deduce that
we deduce that ![]()
![]() is prime, so
is prime, so ![]() By the Fermat Little Theorem,
By the Fermat Little Theorem,
![]()
Since ![]() is the order of
is the order of ![]() modulo
modulo ![]() it follows that
it follows that ![]()
Problem 10.
Determine all finite groups which have exactly ![]() conjugacy classes.
conjugacy classes.
Topic: Group Theory, Difficulty Level: Hard
Indian Statistical Institute, ISI MMath 2017 Problem 10 Hints along with Solution & Discussion
Hint 1
Let ![]() be a finite group with exactly
be a finite group with exactly ![]() conjugacy classes. One conjugacy class is always the identity class
conjugacy classes. One conjugacy class is always the identity class ![]() .
.
Hint 2
Let ![]() and
and ![]() be sizes of other two conjugacy classes. Conjugacy classes form a partition of a group, so
be sizes of other two conjugacy classes. Conjugacy classes form a partition of a group, so
![]()
Hint 3
The size of a conjugacy class of ![]() equals to the index of a centralizer of
equals to the index of a centralizer of ![]()
Full Solution
Let ![]() be a finite group with exactly
be a finite group with exactly ![]() conjugacy classes. One conjugacy class is always the identity class
conjugacy classes. One conjugacy class is always the identity class ![]() Let
Let ![]() and
and ![]() be sizes of other two conjugacy classes. Conjugacy classes form a partition of a group, so
be sizes of other two conjugacy classes. Conjugacy classes form a partition of a group, so
![]()
The size of a conjugacy class of ![]() equals to the index of a centralizer of
equals to the index of a centralizer of ![]() i.e. it divides
i.e. it divides ![]() So,
So,
![]()
Further,
![]()
Assume that ![]() Then
Then ![]() i.e.
i.e. ![]()
![]() The only group of order
The only group of order ![]() is the cyclic group
is the cyclic group ![]() It is an abelian group, hence it has exactly 3 conjugacy classes.
It is an abelian group, hence it has exactly 3 conjugacy classes.
Assume that ![]() Then
Then ![]() hence
hence ![]()
![]() If
If ![]() then
then ![]() and
and ![]() The only groups of order 4 are the Klein 4 group or the cyclic group
The only groups of order 4 are the Klein 4 group or the cyclic group ![]() Both are abelian and thus have 4 conjugacy classes.
Both are abelian and thus have 4 conjugacy classes.
If ![]() then
then ![]() and
and ![]() There are two groups of order
There are two groups of order ![]() an abelian group
an abelian group ![]() and a nonabelian group
and a nonabelian group ![]() (permutations on three elements). We check that
(permutations on three elements). We check that ![]() has three conjugacy classes:
has three conjugacy classes:
![]()
The only finite groups with three conjugacy classes are ![]() and
and ![]()
Problem 11.
Let ![]() be a field,
be a field, ![]() a prime integer. Suppose the polynomial
a prime integer. Suppose the polynomial ![]() is reducible in
is reducible in ![]() . Prove that this polynomial has a root in
. Prove that this polynomial has a root in ![]() .
.
Topic: Field Theory, Difficulty Level: Medium
Indian Statistical Institute, ISI MMath 2017 Problem 11 Hints along with Solution & Discussion
Hint 1
In the case ![]() obviously
obviously ![]() is the needed root.
is the needed root.
Hint 2
We assume firther that ![]() Let
Let ![]() be the splitting field of
be the splitting field of ![]() over
over ![]()
Hint 3
Then
![]()
for some ![]()
Full Solution
In the case ![]() obviously
obviously ![]() is the needed root. We assume firther that
is the needed root. We assume firther that ![]() Let
Let ![]() be the splitting field of
be the splitting field of ![]() over
over ![]() Then
Then
![]()
for some ![]() Since the polynomial
Since the polynomial ![]() is reducible, we may relabel its roots in such a way that for some
is reducible, we may relabel its roots in such a way that for some ![]() a polynomial
a polynomial
![]()
is a factor of ![]() i.e.
i.e. ![]() has coefficients in
has coefficients in ![]() . Observe that for each
. Observe that for each ![]()
![]() Consider the free term of
Consider the free term of ![]() It is of the form
It is of the form ![]() Hence,
Hence, ![]() Further,
Further,
![]()
Since ![]() we can find integers
we can find integers ![]() such that
such that
![]()
We have ![]() and
and
![]()
![]() is a root of
is a root of ![]() in
in ![]() .
.
Problem 12.
Let ![]() be a finite-dimensional vector space over a field
be a finite-dimensional vector space over a field ![]() and let
and let ![]() be a linear transformation. Let
be a linear transformation. Let ![]() be a subspace such that
be a subspace such that ![]() . Suppose
. Suppose ![]() is diagonalizable. Is
is diagonalizable. Is ![]() restricted to
restricted to ![]() also diagonalizable?
also diagonalizable?
Topic: Linear Algebra, Difficulty Level: Hard
Indian Statistical Institute, ISI MMath 2017 Problem 12 Hints along with Solution & Discussion
Hint 1
By assumption, ![]() is a direct sum of subspaces
is a direct sum of subspaces
![]()
and on each subspace ![]()
![]() acts as a multiplication by
acts as a multiplication by ![]() all
all ![]() are distinct.
are distinct.
Hint 2
Consider ![]() Then
Then
![]()
for some ![]()
![]() Let
Let ![]() be the number of nonzero summands
be the number of nonzero summands ![]()
Hint 3
By induction on ![]() we will prove that all
we will prove that all ![]() If
If ![]() then
then ![]() and there is nothing to prove.
and there is nothing to prove.
Full Solution
By assumption, ![]() is a direct sum of subspaces
is a direct sum of subspaces
![]()
and on each subspace ![]()
![]() acts as a multiplication by
acts as a multiplication by ![]() all
all ![]() are distinct.
are distinct.
Consider ![]() Then
Then
![]()
for some ![]()
![]() Let
Let ![]() be the number of nonzero summands
be the number of nonzero summands ![]() By induction on
By induction on ![]() we will prove that all
we will prove that all ![]() If
If ![]() then
then ![]() and there is nothing to prove. Assume the result is proved for number of nonzero summands
and there is nothing to prove. Assume the result is proved for number of nonzero summands ![]() and let
and let ![]() Then
Then
![]()
![]()
By inductive assumption, for all ![]()
![]()
Eigenvalues ![]() are distinct, so
are distinct, so ![]() for
for ![]() But then
But then
![]()
This statement shows that in the decomposition
![]()
all summands are in ![]() i.e.
i.e.
![]()
The restriction of ![]() to
to ![]() is diagonalizable.
is diagonalizable.

Hi! Thanks for your selfless help by putting out all the solutions free of cost on a public domain. I really appreciate it and I’m extremely thankful.
I have a doubt. Can you please explain the reasoning behind the first hint of problem 9?
This is trivially seen from the result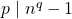 . If
. If  then it implies that
then it implies that 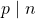 and so
and so 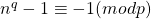 .
.
In problem 10, in the case when m<n, I understood that m+1 should be less than or equal to n.
But how did we immediately get in the next step, that n = m+1 ?
Since then from that it implies
then from that it implies 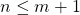 and thus the conclusion.
and thus the conclusion.
Understood both of them, thanks!
In Q.12. Why have we assumed that all eigenvalues are distinct, when we may have a diagonalizable linear transformation on V which has repeated eigenvalues as long as the sum of dimensions of the eigenspaces is dim(V)?