Indian Statistical Institute, ISI BStat & BMath 2023 UGA Solutions & Discussions

Fractions > Indian Statistical Institute, ISI BStat & BMath 2023 UGA Solutions & Discussions

ISI BMATH & BSTAT 2023 Multiple Choice Questions UGA, Objectives: Solutions and Discussions

Past Year’s BMATH/BSTAT Papers & Solutions: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2023 All UGB Objective Solutions: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2021 All UGA Objective Solutions: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2020 All UGA Objective Solutions: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2020 All UGB Subjective Solutions: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2020 UGA Answer Keys: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2020 UGA Question Paper: Click Here

Indian Statistical Institute,ISI BMATH/BSTAT 2020 UGB Question Paper: Click Here

Problem 1

For a real number $x$

$x^3-7 x+6>0$

if and only if

(a) $x>2$

(b) $3-<x<1$

(d) $-3<x<1$ or $x>2$

Solution:

We note that $x=1$ is a root of $x^3-7x+6.$ Hence, we can factor the expression $x^3-7x+6$ as follows:

$\begin{aligned} x^3-7x+6&=\left(x-1+1\right)^3-7(x-1)-7+6\\ &=\left(x-1\right)^3+3\left(x-1\right)^2+3(x-1)+1-7(x-1)-1\\ &=(x-1)\left(\left(x-1\right)^2+3(x-1)-4\right)\\ &=(x-1)(x^2-2x+1+3x-7)=(x-1)(x^2+x-6)\\ &=(x+3)(x-1)(x-2) \end{aligned}$

This expression is positive for $x>2$ and for $x\in (-3,1).$

Answer: (D)

Problem 2

Diefne a polynomial $f(x)$ by

$f(x)=\left|\begin{array}{lll} 1 & x & x \\ x & 1 & x \\ x & x & 1 \end{array}\right|$

for all $x \in \mathbb{R}$ , where the right hand side above is a determinant. Then the roots of $f(x)$ are of the form

(a) $\alpha, \beta \pm i \gamma$ where $\alpha, \beta, \gamma \in \mathbb{R}, \gamma \neq 0$ and $i$ is a square root of $-1 .$

(b) $\alpha, \alpha, \beta$ where $\alpha, \beta \in \mathbb{R}$ are disdinct.

(d) $\alpha, \alpha, \alpha$ for some $\alpha \in \mathbb{R}$

Solution:

Multiplying the first column by $x$ and subtracting it from the second and the third columns we rewrite the determinant as

$\begin{aligned} f(x)&=\left|\begin{matrix} 1 & 0 & 0\\ x & 1-x^2 & x-x^2 \\ x & x-x^2 & 1-x^2 \end{matrix}\right|=\left|\begin{matrix} 1-x^2 & x-x^2 \\ x-x^2 & 1-x^2 \end{matrix}\right| \\ & =\left|\begin{matrix} (1-x)(1+x) & x(1-x) \\ x(1-x) & (1-x)(1+x) \end{matrix}\right|=(1-x)^2\left|\begin{matrix} 1+x & x \\ x & 1+x \end{matrix}\right|=(1-x)^2(1+2x) \end{aligned}$

So, the roots of $f(x)$ are $1,1,-\frac{1}{2}.$

Answer: (B)

Problem 3

Let $S$ be the set of those real numbers $x$ for which the identity

$\sum_{n=2}^{\infty} \cos ^n x=(1+\cos x) \cot ^2 x$

is valid, and the quantities on both sides are finite. Then

(a) $S$ is the empty set

(b) $S=\{x \in \mathbb{R}: x \neq n \pi \text { for all } n\in \mathbb{Z}\}$

(d) $S=\{x \in \mathbb{R}: x \neq (2n+1) \pi \text { for all } n\in \mathbb{Z}\}$

Solution:

If $x=2 k \pi,$ then $\cos^n x=1$ and the series $\sum^\infty_{n=2}\cos^n x$ diverges. If $x=(2k+1) \pi,$ then $\cos^n x=(-1)^n$ and the series $\sum^\infty_{n=2}\cos^n x$ diverges. Assuming that $x\ne \pi k$ for integer values of $k$
we will prove that the identity holds. The series $\sum^\infty_{n=2}\cos^n x$ is a geometric series with the start value $\cos^2 x$ and common ratio $\cos x,$ $|\cos x|<1,:$

$\begin{aligned} \sum^\infty_{n=2}\cos^n x&=\frac{\cos^2 x}{1-\cos x}=\frac{(1+\cos x)\cos^2 x}{(1+\cos x)(1-\cos x)}=\frac{(1+\cos x)\cos^2 x}{1-\cos^2 x}\\ &=\frac{(1+\cos x)\cos^2 x}{\sin^2 x}=(1+\cos x)\cot^2 x \end{aligned}.$

Answer: (B)

Problem 4

The number of consecutive zeroes adjacent to the dignt in the unit’s place of $401^{50}$ is

(a) $3$ ;

(b) $4$ ;

(d) $50$ .

Solution:

By the binomial formula,

$401^{50}=\left(400+1\right)^{50}=\sum^{50}_{n=0} {50 \choose n} 400^n$

Consider first three terms separately:

$401^{50}=1+50\times 400+\frac{50\times 49}{2}\times 400^2+\sum^{50}_{n=3} {50 \choose n} 400^n=196020001+\sum^{50}_{n=3} {50 \choose n} 400^n.$

Note that $\sum^{50}_{n=3} {50 \choose n} 400^n$ is divisible by $1000000.$ It follows that $401^{50}$ ends in $20001.$

Answer: (A)

Problem 5

Consider a right angled triangle $\triangle A B C$ whose hypotenuse $A C$ is of length 1. The bisector of $\angle A C B$ intersects $A B$ at $D$ . If $B C$ is of length $x$ , then what is the length of CD?

(a) $\sqrt{\frac{2 x^2}{1+x}}$

(b) $\sqrt{\frac{1}{2+2x}}$

(d) $\sqrt{\frac{x}{1-x^2}}$

Solution:

Denote the length of $CD$ by $a:$

If $\alpha$ is the angle $\angle DCB,$ then the angle $\angle ACB$ is $2\alpha.$ From triangle $DBC$ we find that

$\frac{x}{a}=\cos \alpha.$

From triangle $ACB$ we find that

$x=\cos 2\alpha=2\cos^2\alpha-1=2\frac{x^2}{a^2}-1.$

Hence,

$x+1=\frac{2x^2}{a^2}, \ a=\sqrt{\frac{2x^2}{x+1}}.$

Answer: (A)

Problem 6

Consider a triangle with vertices $(0,0),(1,2)$ and $(-4,2)$ , Let $A$ be the area of the triangle and $B$ be the area of the circumcircle of the triangle. Then $\frac{B}{A}$ equals

(a) $\frac{\pi}{2}$

(b) $\frac{5\pi}{4}$

(d) $2\pi$

Solution:

The triangle is right angled. Indeed, vectors $(1,2)$ and $(-4,2)$ are orthogonal:

$1\times (-4)+2\times 2=-4+4=0.$

The length of the hypotenuse equals $1+4=5.$ Hence the radius of the circumcircle is $\frac{5}{2}$ and the area of the circumcircle is

$B=\frac{25}{4}\pi.$

Length of catheti are

$\sqrt{1+2^2}=\sqrt{5}, \ \sqrt{4^2+2^2}=\sqrt{20}.$

Hence the area of the triangle is

$A=\frac{1}{2}\sqrt{5\times 20}=5.$

We can find the ratio: $\frac{B}{A}=\frac{5}{4}\pi.$

Answer: (B)

Problem 7

Let $f, g$ be continuous functions from $[0, \infty)$ to itself

$\begin{aligned} & h(x)=\int_{2^x}^{3^x} f(t) dt, x>0 \\ & \text { and } \\ & F(x)=\int_0^{h(x)} g(t) dt, x>0 . \\ & \end{aligned}$

If $F^{\prime}$ is the derivative of $F$ , then for $x>0$ .

(a) $F^{\prime}(x)=g(h(x))$ .
(b) $F^{\prime}(x)=g(h(x))\left[f\left(3^x\right)-f\left(2^x\right)\right]$ .
(c) $F^{\prime}(x)=g(h(x))\left[x 3^{x-1} f\left(3^x\right)-x 2^{x-1} f\left(2^x\right)\right]$ .
(d) $F^{\prime}(x)=g(h(x))\left[3^x f\left(3^x\right) \ln 3-2^x f\left(2^x\right) \ln 2\right]$ .

Solution:

The derivative of $F$ is computed as the derivative of a composite function (using the rule of differentiation of an integral):

$F'(x)=g(h(x))h'(x).$

Further, derivative of $h$ is also computed as the derivative of a composite function:

$h'(x)=f(3^x)3^x\ln 3 -f(2^x) 2^x\ln 2.$

We get

$F'(x)=g(h(x))\left[3^x f(3^x)\ln 3-2^x f(2^x)\ln 2\right].$

Answer: (D)

Problem 8

How many numbers formed by rearranging the digits of 234578 are divisible by $55 ?$

(a) $0$ ;

(b) $12$ ;

(d) $72$ .

Solution:

Consider one number $a_1a_2a_3a_4a_5a_6$ obtained by rearraging digits $2,3,4,5,7,8.$ This number is divisible by $11$ if and only if sums of digits $a_1+a_3+a_5$ and $a_2+a_4+a_6$ differ by a multiple of $11.$ The smallest possible sum of three digits among $2,3,4,5,7,8$ is $2+3+4=9.$ The largest possible sum of three digits among $2,3,4,5,7,8$ is $5+7+8=20.$ No sum of three digits among $2,3,4,5,7,8$ can be equal to the sum of other three digits. Indeed, there are three even and three odd digits. If the sum of three digits among $2,3,4,5,7,8$ is even, then the sum of other three digits must be odd, and vice versa. The difference between two such sums is at most $20-9=11.$ Hence, we will have divisibility by $11$ if and only if either $a_1,a_3,a_5$ are chosen from $2,3,4,$ and $a_2,a_4,a_6$ are chosen from $5,7,8,$ or $a_1,a_3,a_5$ are chosen from $5,7,8,$ and $a_2,a_4,a_6$ are chosen from $2,3,4.$ To get divisibility by $5$ we must have $a_6=5.$ Hence, we will have divisibility by $11$ if and only if $a_1,a_3,a_5$ are chosen from $2,3,4,$ and $a_2,a_4$ are chosen from $7,8.$ Thus, there are

$3!\times 2!=12$

numbers formed by rearraging the digits $2,3,4,5,7,8$ that are divisible by $55.$

Answer: (B)

Problem 9

Let

$S=\left\{\left(\theta \sin \frac{\pi \theta}{1+\theta}, \frac{1}{\theta} \cos \frac{\pi \theta}{1+\theta}\right): \theta \in \mathbb{R}, \theta>0\right\}$

and

$T=\left\{(x, y): x \in \mathbb{R}, y \in \mathbb{R}, x y=\frac{1}{2}\right\} .$

How many elements does $S \cap T$ have?

(a) $0$

(b) $1$

(d) $3$

Solution:

Assume that $(x,y)\in S\cap T.$ Then for some real $\theta>0,$

$x=\theta \sin\frac{\pi \theta}{1+\theta}, \ y=\frac{1}{\theta}\cos\frac{\pi \theta}{1+\theta},$

and

$\frac{1}{2}=xy=\sin\frac{\pi \theta}{1+\theta}\cos \frac{\pi \theta}{1+\theta}.$

It follows that

$1=2\sin\frac{\pi \theta}{1+\theta}\cos \frac{\pi \theta}{1+\theta}=\sin\frac{2\pi\theta}{1+\theta}.$

The latter equality is true if and only if

$\frac{2\pi \theta}{1+\theta}=\frac{\pi}{2}+2\pi k$

for some integer $k.$ Equivalently,

$k=-\frac{1}{4}+\frac{\theta}{1+\theta}.$

Since $0<\frac{\theta}{1+\theta}<1,$ we get

$-\frac{1}{4}<k<\frac{3}{4}.$

The only such integer is $k=0.$ Hence,

$\frac{\theta}{1+\theta}=\frac{1}{4}, \ \theta=\frac{1}{3}.$

There is only one element in $S\cap T,$ namely $\left(\frac{1}{3}\sin \frac{\pi}{4}, 3\cos\frac{\pi}{4}\right).$

Answer: (B)

Problem 10

The limit

$\lim _{n \rightarrow \infty} n^{-\frac{3}{2}}\left((n+1)^{(n+1)}(n+2)^{(n+2)} \ldots(2 n)^{(2 n)}\right)^{\frac{1}{n^2}}$

equals

(a) $0$

(b) $1$

(d) $4e^{-\frac{3}{4}}$

Solution:

We take the logarithm and perform the following transformations:

$-\frac{3}{2}\ln n+\sum^n_{k=1}\frac{n+k}{n^2}\ln \left(n+k\right)=$

$=-\frac{3}{2}\ln n+\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\ln \left(n\left(1+\frac{k}{n}\right)\right)=$

$=-\frac{3}{2}\ln n+\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\left[\ln n +\ln \left(1+\frac{k}{n}\right)\right]=$

$=\ln n \left[-\frac{3}{2}+\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\right]+\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\ln \left(1+\frac{k}{n}\right)=$

$=\ln n \left[-\frac{3}{2}+\frac{1}{n}\left(n+\frac{n(n+1)}{2n}\right)\right]+\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\ln \left(1+\frac{k}{n}\right)=$

$=\ln n \left[-\frac{3}{2}+\frac{3n^2+n}{2n^2}\right]+\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\ln \left(1+\frac{k}{n}\right)=$

$=\frac{\ln n}{2n} +\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\ln \left(1+\frac{k}{n}\right).$

The first summand converges to zero, while the second summand is the integral sum for the integral $\int^2_1 x\ln x dx.$

Hence,

$\lim_{n\to\infty}\frac{1}{n}\sum^n_{k=1}\left(1+\frac{k}{n}\right)\ln \left(1+\frac{k}{n}\right)=\int^2_1 x\ln x dx=$

integrate by parts with $u=\ln x,$ $dv=xdx,$ $du=\frac{dx}{x},$ $v=\frac{x^2}{2}$

$=\frac{x^2}{2}\ln x \bigg|^{2}_1-\int^2_1 \frac{x}{2}dx=\left(\frac{x^2}{2}\ln x-\frac{x^2}{4}\right)\bigg|^2_1=$

$=2\ln 2-1+\frac{1}{4}=2\ln 2-\frac{3}{4}.$

Taking exponent we obtain the needed limit: $2^2e^{-\frac{3}{4}}=4e^{-\frac{3}{4}}.$

Answer: (D)

Problem 11

Suppose $x$ and $y$ are positive integers. If $4 x+3 y$ and $2 x+4 y$ are divided by 7 , then the respective remainders are 2 and 5 . If $11 x+5 y$ is divided by 7 , then the remainder equals

(a) $0$

(b) $1$

(d) $3$

Solution:

Modulo $7$ we have

$5y =2(2x+4y)-(4x+3y)\equiv 2\times 5-2\equiv 8 \equiv 1 \mod 7,$

$y\equiv 15y\equiv 3 \mod7,$

$4\equiv 8x+6y\equiv x+18\equiv x+4 \mod 7,$

$x\equiv 0 \mod 7.$

Hence,

$11x+5y\equiv 5y\equiv 1 \mod 7.$

Answer: (B)

Problem 12

The value of

$\sum_{k=0}^{202}(-1)^k\left(\begin{array}{c} 202 \\ k \end{array}\right) \cos \left(\frac{k \pi}{3}\right)$

equals

(a) $\sin \left(\frac{202}{3} \pi\right)$ .
(b) $-\sin \left(\frac{202}{3} \pi\right)$
(c) $\cos \left(\frac{202}{3} \pi\right)$ .
(d) $\cos ^{202}\left(\frac{\pi}{3}\right)$ .

Solution:

The expression under consideration is the real part of

$\sum^{202}_{k=0}(-1)^k{202 \choose k} e^{\frac{ik\pi}{3}}=$

by the binomial identity

$=\left(1-e^{\frac{i\pi }{3}}\right)^{202}=e^{-\frac{202i\pi}{3}},$

where the latter equality follows from the relation $e^{\frac{i\pi}{3}}+e^{-\frac{i\pi}{3}}=2\cos\frac{\pi}{3}=1.$ Hence, the value of the sum is $\cos\frac{202\pi}{3}.$

Answer: (C)

Problem 13

For real numbers $a, b, c, d, a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}$ , consider the system of equations

$\begin{aligned} a x^2+a y^2+b x+c y+d & =0 \\ a^{\prime} x^2+a^{\prime} y^2+b^{\prime} x+c^{\prime} y+d^{\prime} & =0 . \end{aligned}$

If $S$ denotes the set of all real solutions $(x, y)$ of the above system of equations, then the number of elements in $S$ can never be

(a) $0$
(b) $1$
(c) $2$
(d) $3$

Solution:

The number of solutions to the system of equations

$\begin{cases} ax^2+ay^2+bx+cy+d=0 \\ a'x^2+a'y^2+b'x+c'y+d'=0 \end{cases}$

can never be $3.$ In the following we assume that solutions exist.

Indeed, the first equation is either always holds (if $a=b=c=d=0$ ), or represents a line (if $a=0,$ $b$ and $c$ are not simultaneously zeroes), or represents a circle. Consider the latter case when $a\ne 0.$ Then the first equation takes the form

$x^2+\frac{b}{a}x+y^2+\frac{c}{a}y+\frac{d}{a}=0,$

$(x-\alpha)^2+(y-\beta)^2=R^2,$

where $\alpha=-\frac{b}{2a},$ $\beta=-\frac{c}{2a},$ $R^2=\frac{b^2+c^2}{4a^2}-\frac{d}{a}$ (note that $\frac{b^2+c^2}{4a^2}-\frac{d}{a}> 0,$ as we assume that there are solutions to this equation).

Similarly, the second equation is either always holds (if $a'=b'=c'=d'=0$ ), or represents a line (if $a'=0,$ $b'$ and $c'$ are not simultaneously zeroes), or represents a circle (if $a'\ne 0$ ).

If one of the equations always holds, then the other has infinitely many solutions (as it is either always true, or represents a line, or represents a circle). If both are equations of lines, then either these lines coincide and we get infinitely many solutions, or these lines are different and we get at most one solution. If both are equations of circles, then either these circles coincide and we get infinitely many solutions, or these circles are different and we get at most two solutions. If one equation represents a line, and the other represents a circle, we get at most two solutions.

Answer (D)

Problem 14

The limit

$\lim _{x \rightarrow 0} \frac{1}{x}\left(\cos (x)+\cos \left(\frac{1}{x}\right)-\cos (x) \cos \left(\frac{1}{x}\right)-1\right)$

(a) equals 0 .
(b) equals $\frac{1}{2}$ .
(c) equals 1.
(d) does not exist.

Solution:

Rewrite the expression as

$\frac{1}{x}\left(\cos x-1+\cos\frac{1}{x}\left(1-\cos x\right)\right)=\frac{\cos x -1}{x}\left(1-\cos\frac{1}{x}\right).$

It can be bounded as follows

$\left|\frac{1}{x}\left(\cos x-1+\cos\frac{1}{x}\left(1-\cos x\right)\right)\right|\leq 2\left|\frac{\cos x-1}{x}\right|.$

Hence, the limit is zero, as $\lim_{x\to 0}\frac{\cos x-1}{x}=\sin 0=0.$

Answer: (A)

Problem 15

Let $n$ be a positive integer having 27 divisors including 1 and $n$ , which are denoted by $d_1, \ldots, d_{27}$ . Then the product of $d_1, d_2, \ldots, d_{27}$ equals

(a) $n^{13}$ .
(b) $n^{14}$ .
(c) $n^{\frac{27}{2}}$ .
(d) $27 n$ .

Solution:

For a positive integer $n$ denote by $d(n)$ the number of positive divisors of $n$ (including $1$ and $n$ ). $d$ is a positive divisor of $n$ if and only if $\frac{n}{d}$ is a positive divisor of $n.$ Hence,

$\left(\prod_{d|n} d\right)^2=\prod_{d|n} d\prod_{d|n}\frac{n}{d}=\prod_{d|n}d\frac{n}{d}=\prod_{d|n}n=n^{d(n)}.$

It follows that the product of all positive divisors of $n$ equals $n^{\frac{d(n)}{2}}.$ In our case we get $d_1\ldots d_{27}=n^{\frac{27}{2}}.$

Answer: (C)

Problem 16

Suppose $F: \mathbb{R} \rightarrow \mathbb{R}$ is a continuous function which has exactly one local maximum. Then which of the following is true?

(a) $F$ cannot have a local minimum.
(b) $F$ must have exactly one local minimum.
(c) $F$ must have at least two local minima.
(d) $F$ must have either a global maximum or a local minimum.

Solution:

Let $x_1$ be a single point of local maximum of $F.$ Necessarily, $x_1$ is a point of strict local maximum. Assume that $F$ has no global maximum. Then there exists a point $x_2,$ such that $F(x_2)>F(x_1).$ If $x_2>x_1,$ then, since $F(y)<F(x_1)$ for some $y\in (x_1,x_2),$ the function $F$ attains a local minimum in $(x_1,x_2).$ If $x_2<x_1,$ then, since $F(y)<F(x_1)$ for some $y\in (x_2,x_1),$ the function $F$ attains a local minimum in $(x_2,x_1).$ So, necessarily $F$ has a point of local minimum.

Answer: (D)

Problem 17

Suppose $z \in \mathbb{C}$ is such that the imaginary part of $z$ is non-zero and $z^{25}=1$ . Then

$\sum_{k=0}^{2023} z^k$

equals

(a) $0$ .
(b) $1$ .
(c) $-1-z^{24}$
(d) $-z^{24}$ .

Solution:

Summing the geometric series we get

$\sum^{2023}_{k=0}z^k=\frac{z^{2024}-1}{z-1}=$

we note that $z^{2025}=z^{81\times 25}=1,$ $z^{2024}=\frac{1}{z}$

$=\frac{\frac{1}{z}-1}{z-1}=-\frac{1}{z}=-\frac{z^{25}}{z}=-z^{24}.$

Answer: (D)

Problem 18

Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a twice differentiable one-to-one function. If $f(2)=2, f(3)=-8$ and

$\int_2^3 f(x) d x=-3$

then

$\int_{-8}^2 f^{-1}(x) d x$

equals

(a) -25 .
(b) 25 .
(c) -31
(d) 31.

Solution:

We change variables $y=f^{-1}(x).$ Then $f(y)=x,$ $dx=f'(y)dy.$ If $x=-8,$ then $y=3.$ If $x=2,$ then $y=2.$ Hence

$\int^2_{-8}f^{-1}(x)dx=\int^2_3 yf'(y)dy=$

integrate by parts with $u=y,$ $dv=f'(y)dy,$ $du=dy,$ $v=f(y)$

$=yf(y)\bigg|^{2}_3-\int^2_3 f(y)dy=2f(2)-3f(3)+\int^3_2 f(y)dy=4+24-3=25.$

Answer: (B)

Problem 19

If $f:[0, \infty) \rightarrow \mathbb{R}$ is a continuous function such that

$f(x)+\ln 2 \int_0^x f(t) d t=1, x \geq 0,$

then for all $x \geq 0$ ,

(a) $f(x)=e^x \ln 2$ .
(b) $f(x)=e^{-x} \ln 2$ .
(c) $f(x)=2^x$ .
(d) $f(x)=\left(\frac{1}{2}\right)^x$ .

Solution:

At first we note that $f(0)=1.$ The function $\int^x_0 f(t)dt$ is differentiable, hence $f$ is differentiable as well. For $x>0$ we find from the given equation that

$f'(x)=-\ln 2f(x),$

i.e. $f(x)=f(0) e^{-x \ln 2 }=\left(\frac{1}{2}\right)^x.$

Answer: (D)

Problem 20

If $[x]$ denotes the largest integer less than or equal to $x$ , then

$\left[(9+\sqrt{80})^{20}\right]$

equals

(a) $(9+\sqrt{80})^{20}-(9-\sqrt{80})^{20}$ .
(b) $(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}-20$ .
(c) $(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}-1$ .
(d) $(9-\sqrt{80})^{20}$ .

Solution:

At first we note that $f(0)=1.$ The function $\int^x_0 f(t)dt$ is differentiable, hence $f$ is differentiable as well. For $x>0$ we find from the given equation that

$f'(x)=-\ln 2f(x),$

i.e. $f(x)=f(0) e^{-x \ln 2 }=\left(\frac{1}{2}\right)^x.$

{\bf Answer:} (D)

\item The number $(9+\sqrt{80})^{20}$ is not an integer. Indeed,

$(9+\sqrt{80})^{20}=(9+4\sqrt{5})^{20}=(2+\sqrt{5})^{40}=$

$=\sum^{40}_{k=0}{40\choose k}5^{\frac{k}{2}}2^{40-k}=\sum^{20}_{k=0}{40\choose 2k}5^{k}2^{40-2k}+\left(\sum^{19}_{k=0}{40\choose 2k+1}5^k2^{40-2k-1}\right)\sqrt{5}.$

The latter expression is not integer, as $\sqrt{5}$ is irrational.

Let $k=\left[(9+\sqrt{80})^{20}\right].$ Then $k$ is an integer such that $k<(9+\sqrt{80})^{20}<k+1.$ We note that $\sqrt{80}<9<\sqrt{80}+1.$ Hence, $0<(9-\sqrt{80})^{20}<1.$ The number $(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}$ is integer. Indeed,

$(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}=\sum^{20}_{k=0}{20 \choose k}(1+(-1)^k)80^{\frac{k}{2}}9^{20-k}=$

$=2\sum^{10}_{k=0}{20\choose 2k}80^k 9^{20-2k}.$

Further,

$(9+\sqrt{80})^{20}<(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}<(9+\sqrt{80})^{20}+1,$

$(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}-1<(9+\sqrt{80})^{20}<(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}.$

The integer part of $(9+\sqrt{80})^{20}$ equals $(9+\sqrt{80})^{20}+(9-\sqrt{80})^{20}-1.$

Answer: (C)

Problem 21

The Limit

$\lim_{n\to\infty}\left(2^{-2^{n+1}}+2^{-2^{n-1}}\right)^{2^{-n}}$

equals

(a) $1$

(b) $\frac{1}{\sqrt{2}}$

(d) $\frac{1}{4}$

Solution:

Denote $x=2^n.$ Then

$\lim_{n\to\infty}\left(2^{-2^{n+1}}+2^{-2^{n-1}}\right)^{2^{-n}}=\lim_{x\to\infty}\left(2^{-2x}+2^{-\frac{1}{2}x}\right)^{\frac{1}{x}}.$

The logarithm of this expression equals

$\frac{1}{x}\ln\left(2^{-2x}+2^{-\frac{1}{2}x}\right)=\frac{1}{x}\ln\left(2^{-\frac{1}{2}x}\left(2^{-\frac{3}{2}x}+1\right)\right)=$

$=-\frac{x}{2x}\ln 2+\frac{\ln\left(1+2^{-\frac{3}{2}x}\right)}{x}=-\frac{1}{2}\ln 2+\frac{\ln\left(1+2^{-\frac{3}{2}x}\right)}{2^{-\frac{3}{2}x}}\times \frac{1}{2^{\frac{3}{2}x}x}.$

Since $\lim_{t\to 0}\frac{\ln(1+t)}{t}=1,$ it follows that

$\lim_{x\to\infty} \frac{\ln\left(1+2^{-\frac{3}{2}x}\right)}{2^{-\frac{3}{2}x}}\times \frac{1}{2^{\frac{3}{2}x}x}=0.$

Hence,

$\lim_{n\to\infty}\left(2^{-2^{n+1}}+2^{-2^{n-1}}\right)^{2^{-n}}=\exp\left(-\frac{1}{2}\ln 2+\lim_{x\to\infty} \frac{\ln\left(1+2^{-\frac{3}{2}x}\right)}{2^{-\frac{3}{2}x}}\times \frac{1}{2^{\frac{3}{2}x}x}\right)=2^{-\frac{1}{2}}.$

Answer: (B)

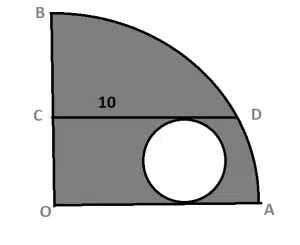
Problem 22

In the following figure, $O A B$ is a quarter-circle. The unshaded region is a circle to which $OA$ and $CD$ are tangents.

If $CD$ is of length 10 and is parallel to $O A$ , then the area of the shaded region in the above figure equals

(a) $25\pi$

(b) $50\pi$

(d) $100\pi$

Solution:

Let $R$ be the radius of the quarter-circle, and $r$ be the radius of the inscribed circle. Consider the right triangle $CDO.$ Its hypotenuse equals $R,$ and its catheti equal $10$ and $2r.$ Hence, $R^2=100+4r^2.$ The area of the quarter-circle equals

$\frac{1}{4}\pi R^2=25\pi +\pi r^2.$

The area of the inscribed circle equals $\pi r^2.$ Hence the area of the shaded region equals $25\pi.$

Answer: (A)

Problem 23

Three left brackets and three right brackets have to be arranged in such a way that if the brackets are serially counted from the left, then the number of right brackets counted is always less than or equal to the number of left brackets counted. In how many ways can this be done?

(a) $3$

(b) $4$

(d) $6$

Solution:

Denote the left bracket by L and the right bracket by R. Let $n_L(k)$ and $n_R(k)$ be the number, respectively, of left and right brackets among first $k$ counted. The first bracket from the left must be L, otherwise we would have $n_L(1)=0<n_R(1).$ If the last bracket is $L,$ then $n_L(6)=2<3=n_R(5).$ Hence, the last bracket must be R. The case $n_L(3)=3$ corresponds to the satisfactory configuration LLLRRR. If $n_L(3)=1,$ then $n_R(3)=2,$ which is not satisfactory. Let $n_L(3)=2.$ Then the first three brackets are either LLR or LRL. Since the last bracket is R, the fourth and fifth bracekts are either LR or RL. In any case we get a satisfactory configuration. So, there are $1+2\times 2=5$ configurations.

Answer: (C)

Problem 24

The polynomial $x^{10}+x^5+1$ is divisible by

(a) $x^2+x+1$ .
(b) $x^2-x+1$ .
(c) $x^2+1$ .
(d) $x^5-1$ .

Solution:

We note that $x^k (x^2+x+1)=x^{k+2}+x^{x+1}+x^k,$ and

$(x^{k}-x^{k-1})(x^2+x+1)=x^{k+2}+x^{x+1}+x^k-x^{k+1}-x^{x}-x^{k-1}=x^{k+2}-x^{k-1}.$

In particular,

$(x^8-x^7)(x^2+x+1)=x^{10}-x^7.$

Further,

$(x^8-x^7+x^5-x^4)(x^2+x+1)=x^{10}-x^7+x^7-x^4=x^{10}-x^4,$

and

$(x^8-x^7+x^5-x^4+x^3)(x^2+x+1)=x^{10}+x^5+x^3.$

Finally,

$(x^8-x^7+x^5-x^4+x^3-x+1)(x^2+x+1)=x^{10}+x^5+x^3-(x^3-1)=x^{10}+x^5+1.$

Answer: (A)

Problem 25

Suppose $a, b, c \in \mathbb{R}$ and

$f(x)=a x^2+b x+c, x \in \mathbb{R}$

If $0 \leq f(x) \leq(x-1)^2$ for all $x$ , and $f(3)=2$ , then

(a) $a=\frac{1}{2}, b=-1, c=\frac{1}{2}$
(b) $a=\frac{1}{3}, b=-\frac{1}{3}, c=0$ .
(c) $a=\frac{2}{3}, b=-\frac{5}{3}, c=1$
(d) $a=\frac{3}{4}, b=-2, c=\frac{5}{4}$ .

Solution:

The function $f$ is a non-zero quadratic function. It is non-linear (as $f(x)\geq 0$ ) and has a unique root (as $f(1)=0$ ). So, $f(x)$ is a square:

$f(x)=a(x-1)^2=ax^2-2ax+a.$

Since $f(3)=2,$ we deduce that $a=\frac{1}{2},$ $b=-1,$ $c=\frac{1}{2}.$

Answer: (A)

Problem 26

As in the following figure, the straight line $O A$ lies in the second quadrant of the $(x, y)$ -plane and makes an angle $\theta$ with the negative half of the $x$ -axis, where $0<\theta<\frac{\pi}{2}$ .

The line segment $C D$ of length 1 slides on the $(x, y)$ -plane in such a way that $C$ is always on $O A$ and $D$ on the positive side of the $x$ -axis. The locus of the mid-point of $C D$ is

(a) $x^2+4 x y \cot \theta+y^2\left(1+4 \cot ^2 \theta\right)=\frac{1}{4}$ .
(b) $x^2+y^2=\frac{1}{4}+\cot ^2 \theta$
(c) $x^2+4 x y \cot \theta+y^2=\frac{1}{4}$ .
(d) $x^2+y^2\left(1+4 \cot ^2 \theta\right)=\frac{1}{4}$ .

Solution:

Denote the length of $OD$ by $t,$ and the length of $OC$ by $a.$ Consider the right triangle $BCD:$

The length of $BD$ equals $t+a\cos \theta.$ The length of $BC$ equals $a\sin\theta.$ Hence,

$(t+a\cos\theta)^2+a^2\sin^2\theta=1,$

$t=\sqrt{1-a^2\sin^2\theta}-a\cos\theta.$

Coordinates of $D$ are $(t,0)=\left(\sqrt{1-a^2\sin^2\theta}-a\cos\theta,0\right).$ Coordinates of $C$ are $(-a\cos\theta,a\sin\theta).$ If $(x,y)$ are coordinates of the mid-point of $CD,$ then

$x=\frac{1}{2}\sqrt{1-a^2\sin^2\theta}-a\cos\theta,\ y=\frac{1}{2}a\sin\theta.$

Hence,

$a=\frac{2y}{\sin\theta},$

$x=\frac{1}{2}\sqrt{1-4y^2}-2y\cot\theta.$

This equality can be transformed as follows

$x^2+4xy\cot\theta+4y^2\cot^2\theta=\frac{1}{4}-y^2,$

$x^2+4xy\cot\theta+y^2\left(1+4\cot^2\theta\right)=\frac{1}{4}.$

Answer: (A)

Problem 27

Suppose that $f(x)=a x^3+b x^2+c x+d$ where $a, b, c, d$ are real numbers with $a \neq 0$ . The equation $f(x)=0$ has exactly two distinct real solutions. If $f^{\prime}(x)$ is the derivative of $f(x)$ , then which of the following is a possible graph of $f^{\prime}(x)$ ?

(a)

(b)

(c)

(d)

Solution:

The function $f(x)$ is a cubic polynomial with real coefficients. Since $f$ has exactly two distinct real roots, all roots are real and one is of order $2.$ Hence, a possible behavior of $f$ is that $f$ increases to one of the roots, then decreases, and then increases intersecting the $x-$ axis again. Correspondingly, the derivative $f'(x)$ is positive, then negative, then positive.

Answer: (B)

Problem 28

Consider the function $f: \mathbb{C} \rightarrow \mathbb{C}$ defined by

$f(a+i b)=e^a(\cos b+i \sin b), a, b \in \mathbb{R}$

where $t$ is a square root of -1 . Then

(a) $f$ is one-to-one and onto.
(b) $f$ is one-to-one but not onto.
(c) $f$ is onto but not one-to-one.
(d) $f$ is neither one-to-one nor onto.

Solution:

We note that $|f(a+ib)|=\sqrt{e^{2a}\cos^2 b+e^{2a}\sin^2 b}=e^a>0.$ In particular, $f(a+ib)\ne 0$ and $f$ is not onto.Since $\cos$ and $\sin$ are $2\pi$ -periodic, $f$ is not one-to-one:

$f(a+i(b+2\pi))=e^a\left(\cos(b+2\pi)+i\sin(b+2\pi)\right)=e^a\left(\cos(b)+i\sin(b)\right)=f(a+ib).$

Answer: (D)

Problem 29

Suppose $f: \mathbb{Z} \rightarrow \mathbb{Z}$ is a non-decreasing function. Consider the following two cases:

$\text{Case 1. } f(0)=2, f(10)=8,$

$\text{Case 2. } f(0)=-2, f(10)=12.$

In which of the above cases it is necessarily true that there exists an $n$ with $f(n)=n$ ?

(a) In both cases.
(b) In neither case.
(c) In Case 1. but not necessarily in Case 2.
(d) In Case 2. but not necessarily in Case 1 .

Solution:

Consider a non-decreasing function $f:\mathbb{Z}\to \mathbb{Z},$ such that $f(0)=2,$ $f(10)=8.$ Assume that $f(n)\ne n$ for all $n.$ We will prove by induction that $f(n)\geq n+1$ for all $n\geq 2.$ Indeed, $f(2)\geq f(0)=2.$ Since $f(2)\ne 2,$ we deduce that $f(2)\geq 3.$ Assume that $f(n)\geq n+1.$ Then $f(n+1)\geq f(n)\geq n+1.$ Since $f(n+1)\ne n+1,$ we deduce that $f(n+1)\geq n+2.$ So, $f(n)\geq n+1$ for all $n\geq 2.$ But this contradicts the property $f(10)=8.$ So, in the Case 1 there must exist $n,$ such that $f(n)=n.$

Consider a function $f:\mathbb{Z}\to \mathbb{Z}$ defined by

$f(n)=\begin{cases} n-1, \ n\leq -2 \\ -2, \ -1\leq n\leq 9 \\ n+2, \ n\geq 10 \end{cases}$

Then $f$ is non-decreasing, $f(0)=-2,$ $f(10)=12,$ but $f(n)\ne n$ for all $n.$

Answer: (C)

Problem 30

How many functions $f:\{1,2, \ldots, 10\} \rightarrow\{1, \ldots, 2000\}$ , which satisfy

$f(i+1)-f(i) \geq 20, \text{for all} 1 \leq i \leq 9,$

are there?

(a) $10 !\left(\begin{array}{c}1829 \\ 10\end{array}\right)$
(b) $11 !\left(\begin{array}{c}1830 \\ 11\end{array}\right)$
(c) $\left(\begin{array}{c}1829 \\ 10\end{array}\right)$
(d) $\left(\begin{array}{c}1830 \\ 11\end{array}\right)$

Solution:

Denote $g(1)=f(1),$ $g(i)=f(i)-f(i-1),$ $2\leq i\leq 10,$ $g(11)=2000-f(10).$ Then we need to find the number of integers solutions of the equation

$g(1)+\ldots+g(11)=2000,$

such that $g(1)\geq 1,$ $g(i)\geq 20,$ $2\leq i\leq 10,$ $g(11)\geq 0.$ Equivalently, if we define $h(1)=g(1),$ $h(i)=g(i)-19,$ $2\leq i\leq 10,$ $h(11)=g(11)+1,$ then we need to find the number of integers solutions of the equation

$h(1)+h(2)+\ldots+h(11)=2000-9\times 19+1=1830,$

where all $h(i)\geq 1.$ The number of solutions is ${1829 \choose 10}.$

Answer: (C)