Problem 1.
Given any set ![]() of
of ![]() points within a unit square, show that there always exists three distinct points in
points within a unit square, show that there always exists three distinct points in ![]() such that the area of the triangle formed by the three points is less than or equal to
such that the area of the triangle formed by the three points is less than or equal to ![]() . (Combinatorics)
. (Combinatorics)
Given any set ![]() of
of ![]() points within a unit square, show that there always exists three distinct points in
points within a unit square, show that there always exists three distinct points in ![]() such that the area of the triangle formed by the three points is less than or equal to
such that the area of the triangle formed by the three points is less than or equal to ![]() . (Combinatorics)
. (Combinatorics)
For every positive integer ![]() , prove that
, prove that
![]()
where ![]() is the sum of all the divisors of
is the sum of all the divisors of ![]() . (Number Theory)
. (Number Theory)
Does there exist non-linear polynomials ![]() and
and ![]() such that
such that ![]() (Polynomials)
(Polynomials)
If ![]() is a twice differentiable function and
is a twice differentiable function and ![]() is continuous on an open interval in
is continuous on an open interval in ![]() , then prove that
, then prove that
![]()
(Calculus)
Thanks sir
Sir..can i submit solution??
Yes, you can type them here.
For the first problem , pigeonhole principle solves the problem quite easily .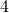 smaller squares of sides of length
smaller squares of sides of length 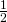 each . By pigeonhole principle , we can say that when 9 points are divided amongst 4 smaller squares , one sqaure must contain
each . By pigeonhole principle , we can say that when 9 points are divided amongst 4 smaller squares , one sqaure must contain 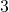 points .
points .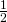 and maximum height is
and maximum height is 

We divide the given square into
Let’s call the square M . In the sqaure M, we join any of the diagonals , and we have a right angle triangle whose maximum base is
So we can conlude that the area has an upper bound of
Yes, you are correct but the result that you are using for the maximum area of a triangle inside a square has to be explicitly explained as to why some other triangles will not have area more than where
where  is the side length of the square.
is the side length of the square.
For the second problem
 .
. occurring
occurring ![Rendered by QuickLaTeX.com [\Floor{\frac{n}{k}}]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-b2792d7523fdbe202cecc2c8fa9dfd07_l3.png) times.
times.
We start by plugging in values .Like for
We notice that all of the fractions are in the form of
Then we have the fraction
Note that![Rendered by QuickLaTeX.com k\times[{\frac{n}{k}}]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-c51173ff86b524b294152f3557fba643_l3.png) , we are basically counting the number of times 1/k occurs.
, we are basically counting the number of times 1/k occurs.
So the sum
And thus proved .
Although the bound is probably even less than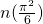
The latex equation got messed up in this one .
I think it’s fine now. Thanks a lot for the discussion. I will comment on the posts tomorrow early morning. Till then solve the rest.
You are absolutely correct. Well done.