ISI MMath Solutions and Discussion 2016 : PMB
ISI MMath PMB 2016 Subjective Questions, solutions and discussions
Sorry, did not get time to post the hints.
To view ISI MMATH 2020 solutions, hints, and discussions: Click Here
To view ISI MMATH 2019 solutions, hints, and discussions: Click Here
To view ISI MMATH 2018 solutions, hints, and discussions: Click Here
To view ISI MMATH 2017 solutions, hints, and discussions: Click Here
To view previous year’s question papers: Click Here
Group A
Problem 1.
Let ![]() be a sequence of real numbers defined as follows:
be a sequence of real numbers defined as follows: ![]() and for all
and for all ![]() .
.
(a)Show that there exists ![]() such that for all
such that for all ![]() ,
,
![]()
(b) Prove that ![]() exists and find its value.
exists and find its value.
Topic: Real Analysis, Difficulty level: Easy
Full Solution
(a) By induction we check that ![]() Indeed, for
Indeed, for ![]() this is true by definition. Assuming that
this is true by definition. Assuming that ![]() we have
we have ![]() hence
hence
![]()
Next, we estimate
![]()
![]()
![]()
The needed estimate holds with ![]()
(b) We have ![]() By induction we check
By induction we check
![]()
For ![]() it is true:
it is true:
![]()
Assuming that ![]() we deduce from (a) that
we deduce from (a) that
![]()
For ![]() we estimate
we estimate
![Rendered by QuickLaTeX.com \[|x_m-x_n|\leq \sum^{m-1}_{k=n}|x_{k+1}-x_k|\leq \frac{1}{4}\sum^{m-1}_{k=n}\lambda^{k-1}\leq \frac{1}{4}\sum^\infty_{k=n}\lambda^{k-1}=\frac{\lambda^{n-1}}{4(1-\lambda)}\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-f8d30c3c39cfdd7963dac6a0fc945693_l3.png)
Since ![]() we deduce that
we deduce that
![]()
i.e. ![]() is a Cauchy sequence and the limit
is a Cauchy sequence and the limit ![]() exists. Passing to the limit in the equation
exists. Passing to the limit in the equation
![]()
we find that
![]()
![]()
![]()
But ![]() for all
for all ![]() So,
So, ![]() and
and
![]()
Problem 2.
Examine, with justification, whether the following limit exists:
![]()
.
If the limit exists, then find its value.
Topic: Real Analysis, Difficulty Level: Easy
Full Solution
Consider the elementary estimate
![]()
Applying it to the integral we get
![]()
![]()
Answer: The limit exists and is equal to zero.
Problem 3.
Does there exist a continuous function ![]() that takes every real value exactly twice
that takes every real value exactly twice ![]() Justify your answer.
Justify your answer.
Topic: Real Analysis, Difficulty Level: Medium
Full Solution
Assume that such a function exists and let ![]() be any of its values. By assumption, there exist
be any of its values. By assumption, there exist ![]() such that
such that
![]()
On the interval ![]() the function
the function ![]() never takes the value
never takes the value ![]() Consequently, either
Consequently, either ![]() for all
for all ![]() or
or ![]() for all
for all ![]() Without loss of generality we can assume that
Without loss of generality we can assume that ![]() for all
for all ![]() (in the opposite case we just consider the function
(in the opposite case we just consider the function ![]()
![]() is also continuous and takes each value exactly twice).
is also continuous and takes each value exactly twice). ![]() reaches maximum on the segment
reaches maximum on the segment ![]() at some point
at some point ![]() Let
Let ![]() For each
For each ![]() we have
we have ![]() so
so ![]() and we necessarily have
and we necessarily have ![]() By assumption, there exists
By assumption, there exists ![]() such that
such that ![]() Observe that
Observe that ![]()
![]() Cconsider two possibilities:
Cconsider two possibilities:
![Rendered by QuickLaTeX.com x_1\not\in [a,b].](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-fd65f66e8faf1ceedfbded87a4ffee80_l3.png) From the Intermediate Value Theorem, any value
From the Intermediate Value Theorem, any value  is reached at least three times: once between
is reached at least three times: once between  and an end-point of
and an end-point of ![Rendered by QuickLaTeX.com [a,b],](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-771abc90d66930a586f12a33ce21ac1c_l3.png) once between
once between 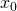 and
and 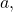 and once between
and once between 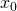 and
and 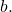 This is impossible.
This is impossible. Then
Then ![Rendered by QuickLaTeX.com f(x_0)=f(x_1)=y_1=\max_{x\in [a,b]}f(x).](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-8a594930d1e24e9b575c7c2990ff8938_l3.png) If
If  is constant between
is constant between 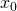 and
and  then the value
then the value  is taken infinitely many times, which is impossible. If
is taken infinitely many times, which is impossible. If  is not constant, there exists
is not constant, there exists  between
between 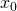 and
and  such that
such that  Fix
Fix  The value
The value  is taken at least four times: between
is taken at least four times: between 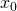 and the end-point of
and the end-point of ![Rendered by QuickLaTeX.com [a,b],](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-771abc90d66930a586f12a33ce21ac1c_l3.png) between
between  and the end-point of
and the end-point of ![Rendered by QuickLaTeX.com [a,b],](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-771abc90d66930a586f12a33ce21ac1c_l3.png) between
between 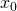 and
and  and between
and between  and
and 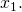
In any case we get a contradiction, so there is no continuous function ![]() that takes every real value exactly twice.
that takes every real value exactly twice.
Problem 4.
Suppose ![]() is a bounded function such that
is a bounded function such that ![]() is Riemann integrable on
is Riemann integrable on ![]() for every
for every ![]() . Is
. Is ![]() Riemann integrable on
Riemann integrable on ![]() ? justify your answer.
? justify your answer.
Topic: Real Analysis, Difficulty Level: Medium
Full Solution
Let ![]() We will prove that
We will prove that ![]() is Riemann integrable by showing that for every
is Riemann integrable by showing that for every ![]() there exists a partition
there exists a partition ![]() of
of ![]() such that for the upper Darboux sum
such that for the upper Darboux sum ![]() and the lower Darboux sum
and the lower Darboux sum ![]() the inequality
the inequality
![]()
holds.
Let ![]() be such that
be such that ![]() Since
Since ![]() is Riemann integrable on
is Riemann integrable on ![]() there exists a partition
there exists a partition ![]() of
of ![]() such that
such that
![Rendered by QuickLaTeX.com \[\sum^n_{j=1}\left(\sup_{x\in [s_{j-1},s_j]}f(x)-\inf_{x\in [s_{j-1},s_j]}f(x)\right)(s_j-s_{j-1})<\frac{\epsilon}{2}.\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-3b566ced14938a2ef86a6062a5471833_l3.png)
Set ![]()
![]()
![]() for
for ![]() so that
so that ![]() Observe that
Observe that
![]()
So,
![Rendered by QuickLaTeX.com \[\sum^{n+1}_{j=1}\left(\sup_{x\in [t_{j-1},t_j]}f(x)-\inf_{x\in [t_{j-1},t_j]}f(x)\right)(t_j-t_{j-1})=\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-cf27ed3b4dffb278e9604d2d7480eb9d_l3.png)
![Rendered by QuickLaTeX.com \[=a\left(\sup_{x\in [t_{0},t_1]}f(x)-\inf_{x\in [t_{0},t_1]}f(x)\right)+\sum^n_{j=1}\left(\sup_{x\in [s_{j-1},s_j]}f(x)-\inf_{x\in [s_{j-1},s_j]}f(x)\right)(s_j-s_{j-1})\leq\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-6f81459132958ec35d4415e3277601da_l3.png)
![]()
![]() is Riemann integrable on
is Riemann integrable on ![]()
Problem 5.
Let ![]() be a surjective function such that
be a surjective function such that
![]()
for all ![]() . Here
. Here ![]() denotes the Euclidean norm on
denotes the Euclidean norm on ![]() . Show that the image of every open set (in
. Show that the image of every open set (in ![]() ) under the map
) under the map ![]() is an open set (in
is an open set (in ![]() ).
).
Topic: Metric Space, Difficulty Level: Medium
Full Solution
Let ![]() be open. Fix
be open. Fix ![]()
![]() for some
for some ![]() There exists
There exists ![]() such that
such that
![]()
Let ![]() By assumption, there exists
By assumption, there exists ![]() such that
such that ![]() We estimate
We estimate
![]()
so,
![]()
and ![]()
![]() We have proved that
We have proved that
![]()
which means that ![]() is open.
is open.
Problem 6.
Suppose that ![]() is a continuous function and
is a continuous function and
![]()
Define a new function ![]() by
by
![]()
Now define another function ![]() by
by
![]()
Does ![]() exist at every point in
exist at every point in ![]() Justify your answer.
Justify your answer.
Topic: Partial Differential, Difficulty Level: High
Full Solution
At first we check that ![]() is continuous. We need two consequences of continuity of
is continuous. We need two consequences of continuity of ![]()
- (boundedness) there exists
 such that
such that  for all
for all ![Rendered by QuickLaTeX.com x,y\in [0,1];](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-27ca775d8ec40a66bf7ece2d78b90ed7_l3.png)
- (uniform continuity) for any
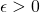 there exists
there exists  such that
such that
![Rendered by QuickLaTeX.com \[x,y,x',y'\in [0,1], |x-x'|\leq \delta, |y-y'|\leq \delta \Rightarrow |g(x,y)-g(x',y')|\leq \epsilon. \eqno(*)\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-c57cefda867db4b97f75d20cb6ab0395_l3.png)
Given ![]() choose
choose ![]() such that (*) holds. Let
such that (*) holds. Let ![]() be such that
be such that ![]()
![]() For any
For any ![]() relation (*) implies
relation (*) implies
![]()
So, we have
![]()
![]()
Continuity of ![]() is proved.
is proved.
For fixed ![]() the function
the function ![]() is continuous on
is continuous on ![]() By the Fundamental Theorem of Calculus, the integral
By the Fundamental Theorem of Calculus, the integral
![]()
is differentiable at ![]() and
and
![]()
So, we`ve proved that
![]()
Group B
Problem 7.
Let ![]() be a
be a ![]() matrix with complex entries. Suppose that
matrix with complex entries. Suppose that ![]() and trace
and trace![]() . Show the following:
. Show the following:
(a) Kernel(A) ![]() Range(A)
Range(A)![]() .
.
(b) ![]() span(Kernel(A)
span(Kernel(A) ![]() Range(A)).
Range(A)).
Topic: Linear Algebra, Difficulty Level: Easy
Full Solution
(a) The characteristic polynomial of ![]() is
is
![]()
So, ![]() has two eigenvalues
has two eigenvalues ![]() and
and ![]() Let
Let ![]() and
and ![]() be corresponding eigenvectors.
be corresponding eigenvectors. ![]() is a basis of
is a basis of ![]() Assume
Assume ![]() Then
Then ![]() for some
for some ![]() and
and ![]() Write
Write ![]() Then
Then
![]()
Since ![]() we deduce
we deduce ![]() and
and ![]()
(b) ![]() so
so ![]() On the other hand
On the other hand ![]() and
and ![]() It follows that
It follows that
![]()
From relation ![]() it follows that the range of
it follows that the range of ![]() is the one-dimensional subspace generated by
is the one-dimensional subspace generated by ![]()
![]()
Finally,
![]()
![]()
![]()
Problem 8.
Suppose that ![]() is a nonzero
is a nonzero ![]() matrix with complex entries. Prove that
matrix with complex entries. Prove that ![]() if and only if the
if and only if the ![]() and the matrix
and the matrix ![]() are similar.
are similar.
Topic: Linear Algebra, Difficulty Level: Medium
Full Solution
Assume that ![]() Consider the Jordan normal form
Consider the Jordan normal form ![]() of the matrix
of the matrix ![]() there exists an invertibale matrix
there exists an invertibale matrix ![]() such that
such that
![]()
and either ![]() or
or ![]() In the first case
In the first case
![]()
Then ![]() and
and ![]() This is not the case.
This is not the case.
Consequently,
![]()
In this case
![]()
and ![]() We have proved that
We have proved that ![]() is similar to the matrix
is similar to the matrix ![]() Observe that for
Observe that for ![]() we have
we have
![]()
![]()
So,
![]()
Conversely, if ![]() is similar to the matrix
is similar to the matrix ![]() then
then ![]() is similar to the matrix
is similar to the matrix
![]()
i.e. ![]()
Problem 9.
Let ![]() be group of all permutation of
be group of all permutation of ![]() distinct symbols. How many subgroups of order
distinct symbols. How many subgroups of order ![]() does
does ![]() have? Justify your answer.
have? Justify your answer.
Topic: Group Theory, Difficulty Level: Medium
Full Solution
A subgroup of prime order is cyclic. Let
![]() be a subgroup of
be a subgroup of ![]() of order
of order ![]() Every element of
Every element of ![]() distinct from the identity is the generator of
distinct from the identity is the generator of ![]() The order of a permutation is the least common mulitple of orders of permutations in its cyckle decomposition. If
The order of a permutation is the least common mulitple of orders of permutations in its cyckle decomposition. If ![]() is a generator, then it is of order
is a generator, then it is of order ![]() and its cycle decomposition consists of a single cycle of length
and its cycle decomposition consists of a single cycle of length ![]()
![]()
Replacing ![]() with
with ![]() for
for ![]() (if needed), we may assume that
(if needed), we may assume that
![]()
There are ![]() such elements and they generate distinct subgroups of order
such elements and they generate distinct subgroups of order ![]() in
in ![]()
Answer: there are ![]() subgroups of order
subgroups of order ![]()
Problem 10.
Suppose that ![]() and
and ![]() are two subgroups of a group
are two subgroups of a group ![]() . Assume that
. Assume that ![]() and
and ![]() is not a subgroup of
is not a subgroup of ![]() . Show that
. Show that ![]()
Topic: Group Theory, Difficulty Level: Easy
Full Solution
Take element ![]() The cosets
The cosets ![]() and
and ![]() are disjoint, so
are disjoint, so ![]() and
and ![]()
Problem 11.
For any ring ![]() , let
, let ![]() denote the ring of all polynomials with indeterminate
denote the ring of all polynomials with indeterminate ![]() and coefficients from
and coefficients from ![]() . Examine, with justification, whether the following pairs of rings are isomorphic:
. Examine, with justification, whether the following pairs of rings are isomorphic:
(a) ![]() and
and ![]() .
.
(b) ![]() and
and ![]()
Topic: Ring Theory, Difficulty Level: Medium
Full Solution
(a) Assume that there exists an isomorphism ![]() Observe that in
Observe that in ![]() we have
we have
![]()
Let ![]() for some
for some ![]() Then
Then
![]()
However, the free term on the left-hand side is ![]()
(b) Consider the mapping ![]() given by
given by
![]()
The mapping ![]() is a surjective homeomoprhism. Indeed, for any
is a surjective homeomoprhism. Indeed, for any ![]() we have
we have
![]()
We find the kernel of ![]()
![]()
![]() and
and ![]() are roots of
are roots of ![]() i.e.
i.e. ![]() is divisible by
is divisible by ![]()
![]()
The kernel of ![]() coincides with the ideal generated by
coincides with the ideal generated by ![]() By the isomoprhism theorem,
By the isomoprhism theorem,
![]()
are isomorphic.
Problem 12.
For any ![]() , let
, let ![]() be the smallest subfield of
be the smallest subfield of ![]() containing
containing ![]() . Find a basis for the vector space
. Find a basis for the vector space ![]() over
over ![]()
Topic: Field Theory, Difficulty Level: Hard
Full Solution
Set ![]() Then
Then
![]()
![]() is a root of the polynomial
is a root of the polynomial
![]()
If we prove that ![]() is irreducible in
is irreducible in ![]() , we will verify that
, we will verify that
![]()
and
![]()
is a basis for the vector space ![]() over
over ![]()
To prove that ![]() is irreducible in
is irreducible in ![]() it is enough to show that the roots
it is enough to show that the roots ![]() do not belong to
do not belong to ![]() Assume that
Assume that
![]()
Then
![]()
![]()
![]()
![]()
![]()
which is impossible as ![]() So,
So, ![]() is irreducible in
is irreducible in ![]()
Answer: ![]() a basis for the vector space
a basis for the vector space ![]() over
over ![]()

Thank you for the solutions. However, I couldn’t find many of these questions in the sample questions/model question paper 2016 that has been uploaded on the official website of ISI, nor could I find them in the list of question papers provided on your website.
May I please know where have you taken these questions from?
Here is the original question paper: https://fractionshub.com/wp-content/uploads/2020/09/MMath-MMTK-PMB-2016.pdf
Also updated the database here: https://fractionshub.com/i-s-i-m-math-previous-years-question/