ISI MMath Solutions and Discussion 2020 : PMB
ISI MMath PMB 2020 Subjective Questions, solutions and discussions
Sorry, did not get time to post the hints.
Question Paper ISI M.Math 2020 PMA Objective Questions Solutions and Discussions: Click Here
To view ISI MMATH 2019 solutions, hints, and discussions: Click Here
To view ISI MMATH 2018 solutions, hints, and discussions: Click Here
To view ISI MMATH 2017 solutions, hints, and discussions: Click Here
To view ISI MMATH 2016 solutions, hints, and discussions: Click Here
To view previous year’s question papers: Click Here
Problem 1.
(a) Let ![]() be a sequence of continuous real-valued functions on
be a sequence of continuous real-valued functions on ![]() converging uniformly on
converging uniformly on ![]() to a function
to a function ![]() . Suppose for all
. Suppose for all ![]() there exists
there exists ![]() such that
such that ![]() . Show that there exists
. Show that there exists ![]() such that
such that ![]() .
.
(b) Give an example of a sequence ![]() of continuous real-valued functions on
of continuous real-valued functions on ![]() converging uniformly on
converging uniformly on ![]() to a function
to a function ![]() , such that for each
, such that for each ![]() there exists
there exists ![]() satisfying
satisfying ![]() , but
, but ![]() satisfies
satisfies ![]() for all
for all ![]() .
.
Topic: Real Analysis, Difficulty level: Medium
Full Solution
(a)
The segment ![]() is compact. Hence, the sequence
is compact. Hence, the sequence ![]() has a convergent subsequence:
has a convergent subsequence:
![]()
The function ![]() is continuous, since it is a uniform limit of continuous functions.
is continuous, since it is a uniform limit of continuous functions.
Let ![]() There exists
There exists ![]() such that for all
such that for all ![]()
![]()
There exists ![]() such that for all
such that for all ![]()
![]() Then we estimate
Then we estimate
![]()
(b)
Let ![]()
![]() We have
We have
![]()
Also, ![]() However,
However, ![]() for all
for all ![]()
It follows that ![]() Since
Since ![]() is arbitrary, we deduce that
is arbitrary, we deduce that ![]()
Problem 2.
Let ![]() be continuous function. Show that
be continuous function. Show that
![]()
Topic: Real Analysis, Difficulty Level: Hard
Full Solution
The function ![]() is bounded on
is bounded on ![]()
![]()
Let ![]() so that for all
so that for all ![]()
![]()
We will use elementary inequality
![]()
Represent the product as
![Rendered by QuickLaTeX.com \[\prod^n_{k=1}\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)=\exp\left(\sum^n_{k=1}\log\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)\right).\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-f2a755244314c6b64900c7cba0a706e0_l3.png)
We have an estimate
![Rendered by QuickLaTeX.com \[\bigg|\sum^n_{k=1}\log\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)-\sum^n_{k=1}\frac{1}{n}f\left(\frac{k}{n}\right)\bigg|\leq\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-339a9640391a8845672529f2624172d7_l3.png)
![Rendered by QuickLaTeX.com \[\leq \sum^n_{k=1}\bigg|\log\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)-\frac{1}{n}f\left(\frac{k}{n}\right)\bigg|\leq 2\sum^n_{k=1}\frac{f(\frac{k}{n})^2}{n^2}\leq \frac{2C^2}{n}.\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-8283cc9be8a0ecc1db49de58a348379e_l3.png)
So,
![Rendered by QuickLaTeX.com \[\sum^n_{k=1}\log\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)-\sum^n_{k=1}\frac{1}{n}f\left(\frac{k}{n}\right)\to 0, \ n\to\infty.\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-9138eb673967e0091270dabe3f92d7a0_l3.png)
Taking into account the convergence
![Rendered by QuickLaTeX.com \[\sum^n_{k=1}\frac{1}{n}f\left(\frac{k}{n}\right)\to \int^1_0 f(x)dx, \ n\to \infty\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-767be1df79b64526834ea1104cc0dc93_l3.png)
we deduce that
![Rendered by QuickLaTeX.com \[\sum^n_{k=1}\log\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)\to \int^1_0 f(x)dx, \ n\to \infty,\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-d86779e7ac9b1dca1a87c579fbadb35d_l3.png)
and finally
![Rendered by QuickLaTeX.com \[\prod^n_{k=1}\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)=\exp\left(\sum^n_{k=1}\log\left(1+\frac{1}{n}f\left(\frac{k}{n}\right)\right)\right)\to \exp\left(\int^1_0 f(x)dx\right),\ n\to\infty.\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-6bf47a335c89a75ff827f6a1c9aaf9bc_l3.png)
Problem 3.
(a) Let ![]() be a twice continuously differentiable function. Show that
be a twice continuously differentiable function. Show that
![]()
for all ![]() .
.
(b) Show that if ![]() further satisfies
further satisfies
![]()
for all ![]() , then there exist
, then there exist ![]() such that
such that ![]() for all
for all ![]() .
.
Topic: Real Analysis, Difficulty Level: Medium
Full Solution
(a)
We use Taylor’s expansion of ![]() with the remainder in the integral form:
with the remainder in the integral form:
![]()
Then
![]()
![]()
![]()
![]()
![]()
We use continuity of second derivative: given ![]() there exists
there exists ![]() such that
such that
![]()
Let ![]() Then
Then
![]()
![]()
since ![]() and
and ![]()
![]()
The convergence
![]()
is proved.
(b)
Differentiate the identity
![]()
with respect to ![]()
![]()
It follows that
![]()
and
![]()
Letting ![]() we deduce
we deduce ![]() So
So ![]()
Problem 4.
Let ![]() be twice continuously differentiable function. Show that if
be twice continuously differentiable function. Show that if ![]() is bounded and
is bounded and ![]() for all
for all ![]() then
then ![]() must be constant.
must be constant.
Topic: Real Analysis, Difficulty Level: Medium
Full Solution
By assumption, the derivative of ![]() is increasing. Assume there exists
is increasing. Assume there exists ![]() such that
such that ![]() Then for all
Then for all ![]()
![]()
It contradicts the fact that ![]() is bounded.
is bounded.
Assume there exists ![]() such that
such that ![]() Then for all
Then for all ![]()
![]()
Again it contradicts the fact that ![]() is bounded. We deduce that
is bounded. We deduce that ![]() and
and ![]() is constant.
is constant.
Problem 5.
Let ![]() be a
be a ![]() real matrix such that
real matrix such that ![]() , where
, where ![]() is the identity matrix
is the identity matrix
(a) Show that if ![]() and
and ![]() , then the vectors
, then the vectors ![]() are linearly independent
are linearly independent
(b) Show that there exists an invertible ![]() real matrix
real matrix ![]() such that
such that
![]()
Topic: Multivariable Calculus, Difficulty Level: Medium
Full Solution
(a)
Assume there are scalars ![]() such that
such that
![]()
Apply ![]() to this equality:
to this equality:
![]()
From these two identities we get
![]()
(b)
Let ![]() be the matrix with the first column given by the vector
be the matrix with the first column given by the vector ![]() and the second column given by the vector
and the second column given by the vector ![]()
![]()
![]() is invertible, since
is invertible, since ![]() is a basis of
is a basis of ![]() Let
Let ![]() Then
Then
![]()
So,
![]()
Since ![]() we get
we get ![]() and
and ![]() Linear independence of
Linear independence of ![]() and
and ![]() are proved.
are proved.
Problem 6.
Suppose ![]() is a
is a ![]() -dimensional real vector space and
-dimensional real vector space and ![]() is a linear map such that
is a linear map such that ![]() and
and ![]() .
.
(a) Show that there exists a vector ![]() such that the set
such that the set ![]() is a basis of
is a basis of ![]() .
.
(b) Suppose ![]() is another linear map such that
is another linear map such that ![]() and
and ![]() . Show that there exists an invertible linear map
. Show that there exists an invertible linear map ![]() such that
such that ![]() .
.
Topic: Linear Algebra, Difficulty Level: Medium
Full Solution
(a)
Let ![]() be such that
be such that ![]() Assume the system
Assume the system ![]() is linearly dependent. Then there are scalars
is linearly dependent. Then there are scalars ![]() such that
such that
![]()
Apply ![]() to this identity and use the fact
to this identity and use the fact ![]()
![]()
Apply ![]() to this identity and use the fact
to this identity and use the fact ![]()
![]()
(b)
Let ![]() be such that
be such that ![]() is a basis of
is a basis of ![]() Let
Let
![]()
be the matrix whose columns are given by vectors ![]() The matrix
The matrix ![]() is invertible. We have
is invertible. We have
![Rendered by QuickLaTeX.com \[TW=\begin{pmatrix}T(v) & T^2(v) & 0 \end{pmatrix} = \begin{pmatrix}v & T(v) & T^2(v) \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0\\ 0 & 1 &0 \end{pmatrix} =W \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0\\ 0 & 1 &0 \end{pmatrix}\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-b4344456c7de4ce6f16b0be4ad206666_l3.png)
It follows that
![Rendered by QuickLaTeX.com \[W^{-1}TW=\begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0\\ 0 & 1 &0 \end{pmatrix}\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-d002732a5afb17781bad8ff78182c900_l3.png)
for some invertible matrix ![]() .
.
If ![]() is another linear map of
is another linear map of ![]() such that
such that ![]() and
and ![]() then for some invertible matrix
then for some invertible matrix ![]() we have
we have
![Rendered by QuickLaTeX.com \[Q^{-1}SQ=\begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0\\ 0 & 1 &0 \end{pmatrix}\]](https://fractionshub.com/wp-content/ql-cache/quicklatex.com-5ae1638ee03d3a6ad0e3efc2588228db_l3.png)
So,
![]()
and
![]()
for ![]()
But ![]() So,
So, ![]() and consequently
and consequently ![]() Linear independence of
Linear independence of ![]() is proved.
is proved.
Problem 7.
Let ![]() be a field, and let
be a field, and let ![]() be the ring
be the ring ![]() . Let
. Let ![]() be the ideal generated by
be the ideal generated by ![]() . Find all maximal ideals of the ring
. Find all maximal ideals of the ring ![]() .
.
Topic: Ring Theory, Difficulty Level: Hard
Full Solution
Consider the mapping ![]() given by
given by
![]()
![]() is a ring homomorphism. The kernel of
is a ring homomorphism. The kernel of ![]() coincides with
coincides with ![]() Indeed,
Indeed,
![]()
Given ![]() consider
consider ![]() Then
Then
![]()
So, ![]() maps
maps ![]() onto
onto ![]() By the isomorphism theorem,
By the isomorphism theorem, ![]() is isomorphic to
is isomorphic to ![]() . Consider a maximal ideal
. Consider a maximal ideal ![]() of
of ![]()
![]() Consider arbitrary nonzero
Consider arbitrary nonzero ![]() Then
Then
![]()
If ![]() and
and ![]() then
then ![]() and
and ![]() In this case
In this case ![]() is not a maximal ideal. So, either
is not a maximal ideal. So, either
![]() or
or ![]()
Conclusion. There are two maximal ideals in ![]() One is generated by
One is generated by ![]() another is generated by
another is generated by ![]()
Problem 8.
Let ![]() be a finite group, and let
be a finite group, and let ![]() be a normal subgroup of
be a normal subgroup of ![]() , Let
, Let ![]() be a Sylow
be a Sylow ![]() -subgroup of
-subgroup of ![]()
(a) Show that for all ![]() , there exists
, there exists ![]() such that
such that ![]() .
.
(b) Let ![]() . Let
. Let ![]() be the set
be the set ![]() . Show that
. Show that ![]() .
.
Topic: Group Theory, Difficulty Level: Easy
Full Solution
(a)
Let ![]()
![]() is a normal subgroup of
is a normal subgroup of ![]() , so
, so
![]()
It follows that ![]() is a subgroup of
is a subgroup of ![]() .
.
But ![]() and
and ![]() is a Sylow
is a Sylow ![]() subgroup of
subgroup of ![]() By Sylow theorem,
By Sylow theorem, ![]() and
and ![]() are conjugate in
are conjugate in ![]() , i.e. there exists
, i.e. there exists ![]() such that
such that
![]()
(b)
Let ![]() There exists
There exists ![]() such that
such that
![]()
Then
![]()
So,
![]()
and
![]()
Equality ![]() is proved.
is proved.

Here is a less elegant solution to Problem 4 which does not require integration:
We first show that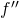 is identically zero. Suppose
is identically zero. Suppose  for some real number
for some real number  . Since
. Since 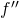 is continuous, there is an open interval
is continuous, there is an open interval  containing
containing  such that
such that  for all
for all  . Thus,
. Thus,  is strictly increasing on
is strictly increasing on  . Let
. Let 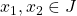 with
with  . Then
. Then  .
. such that
such that
By Taylor's Theorem, there is
Noting that , \frac{f(x_2)-f(x_1)}{x_2-x_1}=f'(x_1)+\frac{(x_2-x_1)}{2}f''(d)f'(d).
, \frac{f(x_2)-f(x_1)}{x_2-x_1}=f'(x_1)+\frac{(x_2-x_1)}{2}f''(d)f'(d). f”(x)=0
f”(x)=0 x
x f(x)=Ax+B
f(x)=Ax+B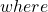 A,B
A,B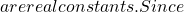 f
f A=0
A=0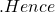 f$ is a constant function.
f$ is a constant function.
I am a little confused about Problem 3 part (a). It can be solved using only L-Hopital’s Rule without using continuity of second derivative. Is there any reason that hypothesis was included?
You are using which can be guranteed by continuity of
which can be guranteed by continuity of 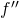
Please solve CMI msc math previous year paper
Official Solutions has already been published by CMI.